Difference between revisions of "SNF P2P"
| (7 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
=Approach= | =Approach= | ||
| + | We first outline new ideas that we will work on with the goal of designing accurate (and profitable) credit risk models. Later, we describe key challenges that we will face in the empirical part of the research, including the planned approach to addressing the issues raised. | ||
| + | |||
| + | ==Network-based credit risk models == | ||
| + | The following ideas present the potential offered by network-based credit risk models that we plan to leverage and represent the backbone of our contribution to the literature on P2P credit risk models. | ||
| + | *The MST used before is a drastic filtering technique that reduces the 2–1[N×(N–1)] pairwise relationships to just (N–1); this might lead to a loss of important network features (e.g., Výrost et al., 2019). Moreover, the MST algorithm requires selecting edges such that all vertices remain connected; thus, the algorithm is topological in nature. This topological condition cannot be translated into a meaningful interpretation in a credit risk context. We will experiment with threshold networks that retain α% ∈ (0, 100) (hyperparameter) of the closest distances. | ||
| + | *P2P data are not only numerical (e.g., loan amount, interest rate, debt to income) but often of a mixed nature and can be transformed to indicator variables (e.g., homeownership, location, job status). Such a transformation increases the number of variables considerably (e.g., after transformation, in the case of the benchmark LC database, the number of variables exceeds 600), which will make subsequent network estimation very expensive in terms of computation power and memory. Moreover, previous studies have relied on the Euclidean distance only, which is not suitable for such mixed data. We will explore heterogeneous distance measures that are suitable for continuous and categorical data, such as the HEOM and HVDM measures of Wilson and Martinez (1997), which are now standard in the machine learning literature. We will also explore recent ensemble distance measures from Ahmad and Dey (2007) and their extension from Harikumar and Surya (2015). | ||
| + | *The α% of a threshold network is a hyperparameter that we plan to optimize through k-fold cross- validation. Various threshold networks have been used before in finance. For example, the Granger causality networks of Billio et al. (2012) are of that form, where the threshold is a random variable. Onnela et al. (2004) used the same principle to create a network, but the number of retained edges was not optimized. Our idea is also similar to work in various research domains in finance, physics or epidemiology where network percolation is studied; i.e., the set of edges is expanded by adding edges starting with the smallest distance d1 < d2 < … until a certain topological property of a network changes. To optimize the α%, we need a loss function (some measure of performance) that will utilize the knowledge about loan default status, thus leading to supervised learning. Here, the possibilities are expansive and lead to multiple research paths: | ||
| + | *#We explore the α% network that will lead to the highest difference between the centrality of defaulted and nondefaulted loans. Several centrality measures, including closeness, betweenness, harmonic centrality and PageRank, can be explored. | ||
| + | *#We explore an α% network that will maximize percolation centrality measures and that utilizes loan default status; i.e., the shortest paths in a network are weighted depending on whether they go through defaulted or nondefaulted loans. | ||
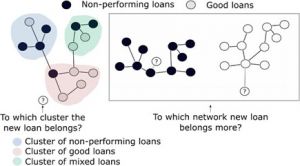
| + | *#We explore an α% network that will lead to clusters that discriminate well between defaulted and nondefaulted loans (see Figure 1, left panel). Specifically, to identify clusters, we will rely on the Louvain method of Blondel et al. (2008). Within a k-fold cross-validation algorithm, new loans are introduced (out-of-sample) to this network, and we need to place (label) each new loan in a certain cluster. This is by itself a challenging task; for example, new loans might be closer to multiple clusters, in which case it seems that a probabilistic assignment is more suitable. To facilitate further discussion, we index each cluster as c = 1, 2, …, in a given α% network of the training sample, new defaulted loans as g = 1, 2, …., ND and nondefaulted loans as j = 1, 2, …, NN. Now, given the cluster to which each new loan belongs, we can find the ratio of defaulted to nondefaulted loans (in the cluster to which the loan belongs) and denote it as Rα%. The average of such ratios only for new defaulted loans (∑g=1 Rα%, g)/ND and the average of ratios only for new nondefaulted loans is (∑j=1 Rα%, j)/NN. We are interested in maxα% → [(∑g=1 Rα%,g)/ND]/[(∑j=1 Rα%,j)/NN]. The idea is that we should work with a network with a hyperparameter α% such that clusters within that network maximize the discrimination between defaulted and nondefaulted loans. | ||
| + | Several other interesting points emerge. For example, we expect that many clusters will not discriminate well between good and bad loans or that some clusters will be sparsely populated, i.e., unstable. A possibility is to introduce a new hyperparameter that selects a certain number of clusters that discriminate well between good and bad loans. Alternatively, we might estimate a statistical benchmark value for the ratio (or even centrality measures as well) that is typical for random networks of similar structure. Such random networks can be formed via exponential random graphs (Robins et al., 2007), which we have used before in the context of banking networks (i.e., Deev and Lyócsa, 2020). [[File:Example_network.jpg|thumb|Figure 1: Example of P2P loan-based networks|link=Special:FilePath/Example_network.jpg]] | ||
| + | *We also plan to explore the possibility of utilizing information from multiple networks within one estimation. The new ideas that we are exploring are as follows: | ||
| + | *#In Giudici et al. (2019a,b), the network was created using all loans in the training set. A semi supervised approach would be able to utilize the information about the loan’s status such that one network is created for defaulted loans only and one for nondefaulted loans only. The idea is that a highly centralized loan in a network of defaulted loans is likely to be easily identified as defaulted. On the other hand, due to unobserved factors, loans on the periphery (i.e., less connected via observed attributes) might be impossible to identify as defaults. The same applies for a network of nondefaulted loans. After a new loan is introduced to both networks, we estimate the extent to which the loan belongs to the defaulted or nondefaulted network (see Figure 1, right panel). The given variable might be based on centralization measures and might also be optimized via k-fold cross- validation. | ||
| + | *#In the creation of a network, it is unclear which and how many variables to use to calculate similarity distances between loans. Interestingly, this step has been left unexplored in the literature. Motivated by the success of bagging in machine learning, we would like to explore several of the previously described ideas within the following framework of multiple networks. Within this framework, we will i) randomly select m variables to create a given network; ii) find measures of interest (clusters, loan centralities for new loans, etc.); iii) repeat the steps i) and ii) n times; and iv) aggregate measures of interest across all networks. In this way, we will account for the variable choice uncertainty and inherent noisiness of the data typical of P2P lending datasets. Alternatively, we might follow a bootstrap aggregation technique: | ||
| + | *##randomly reshuffle the training dataset; | ||
| + | *##select predefined variables to create a given network; | ||
| + | *##find measures of interest | ||
| + | *##repeat steps 1 to 3 n times; | ||
| + | *##aggregate measures of interest across all networks. | ||
| + | In this way, we will account for the uncertainty of the training dataset. Both approaches can be combined as well. We expect that accounting for various sources of uncertainty through aggregation will help us develop more robust network-based features, but we might also be able to understand which variables drive credit risk and what values (thresholds) of various network measures (i.e., vertex centralities) are relevant. | ||
| + | Although these ideas represent the backbone of this research project, over the course of the three years, other new ideas are likely to emerge. | ||
| + | |||
==XAI methods for finance== | ==XAI methods for finance== | ||
In addition to the work on credit scoring models, we will also aim to contribute to the literature on XAI methods applied to financial problem sets. As stated previously, most of the papers available in the literature communicate the results of implementing individual post hoc XAI methods identifying the contribution of individual features to the predicted outcome. Feature importance methods provide explanations by taking a model ƒ and a point of interest x and returning a score reflecting the importance of the attributes for that specific point x. In finance, internal credit risk models are subjected to various audits (risk and legal) and have to “work” within the practical constraints under which banks operate (various unlinked database management systems, inability to transfer original client data to cloud services, etc.). | In addition to the work on credit scoring models, we will also aim to contribute to the literature on XAI methods applied to financial problem sets. As stated previously, most of the papers available in the literature communicate the results of implementing individual post hoc XAI methods identifying the contribution of individual features to the predicted outcome. Feature importance methods provide explanations by taking a model ƒ and a point of interest x and returning a score reflecting the importance of the attributes for that specific point x. In finance, internal credit risk models are subjected to various audits (risk and legal) and have to “work” within the practical constraints under which banks operate (various unlinked database management systems, inability to transfer original client data to cloud services, etc.). | ||
| Line 22: | Line 44: | ||
#''Empirical'' – Almost all studies have used fewer than two P2P market datasets, with three datasets used only occasionally (Ha et al., 2019; Niu et al., 2020). The fourth contribution is to enrich the empirical literature, as we will be able to observe credit drivers and the usefulness of methods across different market platforms. We will use not only benchmark datasets (Lending Club and Prosper) but also new datasets from European (Zopa, Mintos, Bondora) and world (Mintos, Home Credit, Kiva) P2P markets. With this, we will be able to validate models across very different datasets capturing the unique properties of different P2P markets around the world. | #''Empirical'' – Almost all studies have used fewer than two P2P market datasets, with three datasets used only occasionally (Ha et al., 2019; Niu et al., 2020). The fourth contribution is to enrich the empirical literature, as we will be able to observe credit drivers and the usefulness of methods across different market platforms. We will use not only benchmark datasets (Lending Club and Prosper) but also new datasets from European (Zopa, Mintos, Bondora) and world (Mintos, Home Credit, Kiva) P2P markets. With this, we will be able to validate models across very different datasets capturing the unique properties of different P2P markets around the world. | ||
#''Practical'' – Except for a few studies (Bussmann et al. 2019, Srinivasan et al. 2019, Ariza-Garzon et al., 2020, Hadji Misheva et al. 2021 Moscato et al., 2021), the applicability and robustness of the explanations provided by existing XAI methods for credit risk models has rarely been studied. However, the future trend put forward by policymakers and regulators (through existing and planned legislation) concerning automatized solutions and P2P lending markets emphasizes the necessity of interpretable credit risk models. Thus, the fifth contribution of the proposed research project is an investigation into the applicability of existing XAI methods to credit scoring models, which will ultimately enable the development of interpretable credit risk models that can estimate not only the expected effect of each variable on the outcome but also the expected effect of each variable for a specific individual loan | #''Practical'' – Except for a few studies (Bussmann et al. 2019, Srinivasan et al. 2019, Ariza-Garzon et al., 2020, Hadji Misheva et al. 2021 Moscato et al., 2021), the applicability and robustness of the explanations provided by existing XAI methods for credit risk models has rarely been studied. However, the future trend put forward by policymakers and regulators (through existing and planned legislation) concerning automatized solutions and P2P lending markets emphasizes the necessity of interpretable credit risk models. Thus, the fifth contribution of the proposed research project is an investigation into the applicability of existing XAI methods to credit scoring models, which will ultimately enable the development of interpretable credit risk models that can estimate not only the expected effect of each variable on the outcome but also the expected effect of each variable for a specific individual loan | ||
| + | |||
| + | |||
| + | =References= | ||
| + | # Ahmad, A., & Dey, L. (2007). A k-mean clustering algorithm for mixed numeric and categorical data. ''Data & Knowledge Engineering'', 63(2), 503-527. | ||
| + | # Ahelegbey, D. F., & Giudici, P. (2019). Latent factor models for credit scoring in P2P systems. ''Physica A: Statistical Mechanics and its Applications'', 522, 112-121. | ||
| + | # Arya, A., & Giudici, G. (2019). Network based scoring models to improve credit risk management in peer to peer lending platforms. ''Frontiers in Artificial Intelligence'', 2, 3. | ||
| + | # Billio, M., Getmansky, M., Lo, A. W., & Pelizzon, L. (2012). Econometric measures of connectedness and systemic risk in the finance and insurance sectors. ''Journal of financial economics'', 104(3), 535-559. | ||
| + | # Berg, J. E., Easton, P. D., Hill, M. D., & Pyzoha, S. J. (2020). XAI in the Financial Sector. A Conceptual Framework for Explainable AI. | ||
| + | # Blondel, V. D., Guillaume, J. L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. ''Journal of statistical mechanics: theory and experiment'', 2008(10), P10008. | ||
| + | # Bhatt, P., Garg, A., & Mehta, N. (2020). Credit risk evaluation model with textual features from loan descriptions for P2P lending. ''Electronic Commerce Research and Applications'', 42, 100989. | ||
| + | # Deev, O., & Lyócsa, Š. (2020). Connectedness of financial institutions in Europe: A network approach across quantiles. ''Physica A: Statistical Mechanics and its Applications'', 550, 124035. | ||
| + | # Emekter, R., Tu, Y., Jirasakuldech, B., & Lu, M. (2015). Evaluating credit risk and loan performance in online Peer-to-Peer (P2P) lending. ''Applied Economics'', 47(1), 54-70. | ||
| + | # Gao, X., Lu, L., & Chen, Z. (2021). Determinants of defaults on P2P lending platforms in China. ''International Review of Economics & Finance'', 72, 334-348. | ||
| + | # Giudici, G., Wang, Y., & Huang, H. (2019). Network based credit risk models. ''Quality Engineering'', 32(2), 199-211. | ||
| + | # He, Y., & Li, X. (2021). The failure of Chinese peer-to-peer lending platforms: Finance and politics. ''Journal of Corporate Finance'', 66, 101852. | ||
| + | # Jin, Y., & Zhu, Y. (2015, April). A data-driven approach to predict default risk of loan for online peer-to-peer (P2P) lending. In ''2015 Fifth International Conference on Communication Systems and Network Technologies'' (pp. 609-613). IEEE. | ||
| + | # Niu, Q., Xia, H., Li, J., & Cui, Z. (2020). Resampling ensemble model based on data distribution for imbalanced credit risk evaluation in P2P lending. ''Information Sciences'', 536, 120-134. | ||
| + | # Onnela, J. P., Kaski, K., & Kertész, J. (2004). Clustering and information in correlation based financial networks. ''The European Physical Journal B'', 38(2), 353-362. | ||
| + | # Robins, G., Pattison, P., Kalish, Y., & Lusher, D. (2007). An introduction to exponential random graph (p*) models for social networks. ''Social networks'', 29(2), 173-191. | ||
| + | # Thakor, A. V. (2020). Fintech and banking: What do we know? ''Journal of Financial Intermediation'', 41, 100833. | ||
| + | # Výrost, T., Lyócsa, Š., & Baumöhl, E. (2019). Network-based asset allocation strategies. ''The North American Journal of Economics and Finance'', 47, 516-536. | ||
| + | # Wilson, D. L., & Martinez, T. R. (1997). Improved heterogeneous distance functions. ''Journal of artificial intelligence research'', 6, 1-34. | ||
| + | # Xia, H., Li, J., & Niu, Q. (2017). Cost-sensitive boosted tree for loan evaluation in peer-to-peer lending. ''Electronic Commerce Research and Applications'', 24, 30-49. | ||
Latest revision as of 18:47, 30 October 2023
Abstract
P2P (peer-to-peer) lending today consists of the lending of money to individuals and businesses through online services without bank intermediation (Thakor, 2020). P2P platforms offer a secure cyberspace (Niu et al., 2020) where borrowers are linked to investors who engage (usually) in a buyout auction, where the bidding process ends when the loan has been fully funded (Xia et al., 2017). Bank lending is backed by deposits, uninsured debt and equity; thus, banks have skin in the game, unlike P2P lending platforms, where loans are funded by investors directly, i.e., through investors’ equity. Higher interest rates and diversification potential incentivize lenders, represented by individuals and recently also by banks, hedge funds, venture capital firms and private equity firms (Giudici et al. 2019a), to participate in P2P lending. Traditional banks receive loan repayments that are used to pay out depositors, subordinated debt holders and potentially shareholders, while P2P platforms receive fees from loan origination (paid by the borrower) and transaction fees. Administration of lending tends to be cheaper for P2P platforms, which provide an online marketplace and initial risk classification, while banks are subject to much tighter regulation and thus have higher costs (Thakor, 2020). However, banks have much richer data at their disposal (e.g., through long-term relational banking), which makes their task of identifying potential nonperforming loans easier. One would therefore expect P2P platforms to attract borrowers who would otherwise not be eligible for bank loans. This effect is amplified during recessions, as reduced access to bank credit directs riskier borrowers towards the P2P markets. This phenomenon has been observed empirically, as several studies have found that after the 2008 recession, the growth of P2P markets accelerated (e.g., Jin and Zhu, 2015). Similar growth is likely to unfold during and after the current worldwide economic crisis induced by the COVID-19 pandemic.Given the nature of P2P markets, they are characterized as immature industries with loose regulation, greater information asymmetry and increased credit risk, which all lead to higher default rates. This leaves the door open to considerable risks. To mitigate adverse selection and moral hazard problems, one needs to build trust. In traditional bank-lending markets, trust is constructed via relational banking, using collateral, certified accounts, risk monitoring, the presence of a board of directors, tighter regulation, etc. (Emekter, 2015). Voluntary implementation of these mechanisms would incur significant costs and thus marginalize the competitive edge of P2P lending markets. Several recent studies have found that the failure of P2P platforms in China is related to general market conditions (bond yields), ownership, information disclosure, and popularity, while political ties were found to also play an important role (e.g., Gao et al., 2021, He and Li, 2021). A hands-on approach to establishing trust between investors and P2P markets is to use accurate credit risk models. The main objective of the proposed research project is to design a state-of-the art and interpretable credit risk models for P2P lending markets.
Approach
We first outline new ideas that we will work on with the goal of designing accurate (and profitable) credit risk models. Later, we describe key challenges that we will face in the empirical part of the research, including the planned approach to addressing the issues raised.
Network-based credit risk models
The following ideas present the potential offered by network-based credit risk models that we plan to leverage and represent the backbone of our contribution to the literature on P2P credit risk models.
- The MST used before is a drastic filtering technique that reduces the 2–1[N×(N–1)] pairwise relationships to just (N–1); this might lead to a loss of important network features (e.g., Výrost et al., 2019). Moreover, the MST algorithm requires selecting edges such that all vertices remain connected; thus, the algorithm is topological in nature. This topological condition cannot be translated into a meaningful interpretation in a credit risk context. We will experiment with threshold networks that retain α% ∈ (0, 100) (hyperparameter) of the closest distances.
- P2P data are not only numerical (e.g., loan amount, interest rate, debt to income) but often of a mixed nature and can be transformed to indicator variables (e.g., homeownership, location, job status). Such a transformation increases the number of variables considerably (e.g., after transformation, in the case of the benchmark LC database, the number of variables exceeds 600), which will make subsequent network estimation very expensive in terms of computation power and memory. Moreover, previous studies have relied on the Euclidean distance only, which is not suitable for such mixed data. We will explore heterogeneous distance measures that are suitable for continuous and categorical data, such as the HEOM and HVDM measures of Wilson and Martinez (1997), which are now standard in the machine learning literature. We will also explore recent ensemble distance measures from Ahmad and Dey (2007) and their extension from Harikumar and Surya (2015).
- The α% of a threshold network is a hyperparameter that we plan to optimize through k-fold cross- validation. Various threshold networks have been used before in finance. For example, the Granger causality networks of Billio et al. (2012) are of that form, where the threshold is a random variable. Onnela et al. (2004) used the same principle to create a network, but the number of retained edges was not optimized. Our idea is also similar to work in various research domains in finance, physics or epidemiology where network percolation is studied; i.e., the set of edges is expanded by adding edges starting with the smallest distance d1 < d2 < … until a certain topological property of a network changes. To optimize the α%, we need a loss function (some measure of performance) that will utilize the knowledge about loan default status, thus leading to supervised learning. Here, the possibilities are expansive and lead to multiple research paths:
- We explore the α% network that will lead to the highest difference between the centrality of defaulted and nondefaulted loans. Several centrality measures, including closeness, betweenness, harmonic centrality and PageRank, can be explored.
- We explore an α% network that will maximize percolation centrality measures and that utilizes loan default status; i.e., the shortest paths in a network are weighted depending on whether they go through defaulted or nondefaulted loans.
- We explore an α% network that will lead to clusters that discriminate well between defaulted and nondefaulted loans (see Figure 1, left panel). Specifically, to identify clusters, we will rely on the Louvain method of Blondel et al. (2008). Within a k-fold cross-validation algorithm, new loans are introduced (out-of-sample) to this network, and we need to place (label) each new loan in a certain cluster. This is by itself a challenging task; for example, new loans might be closer to multiple clusters, in which case it seems that a probabilistic assignment is more suitable. To facilitate further discussion, we index each cluster as c = 1, 2, …, in a given α% network of the training sample, new defaulted loans as g = 1, 2, …., ND and nondefaulted loans as j = 1, 2, …, NN. Now, given the cluster to which each new loan belongs, we can find the ratio of defaulted to nondefaulted loans (in the cluster to which the loan belongs) and denote it as Rα%. The average of such ratios only for new defaulted loans (∑g=1 Rα%, g)/ND and the average of ratios only for new nondefaulted loans is (∑j=1 Rα%, j)/NN. We are interested in maxα% → [(∑g=1 Rα%,g)/ND]/[(∑j=1 Rα%,j)/NN]. The idea is that we should work with a network with a hyperparameter α% such that clusters within that network maximize the discrimination between defaulted and nondefaulted loans.
Several other interesting points emerge. For example, we expect that many clusters will not discriminate well between good and bad loans or that some clusters will be sparsely populated, i.e., unstable. A possibility is to introduce a new hyperparameter that selects a certain number of clusters that discriminate well between good and bad loans. Alternatively, we might estimate a statistical benchmark value for the ratio (or even centrality measures as well) that is typical for random networks of similar structure. Such random networks can be formed via exponential random graphs (Robins et al., 2007), which we have used before in the context of banking networks (i.e., Deev and Lyócsa, 2020).
- We also plan to explore the possibility of utilizing information from multiple networks within one estimation. The new ideas that we are exploring are as follows:
- In Giudici et al. (2019a,b), the network was created using all loans in the training set. A semi supervised approach would be able to utilize the information about the loan’s status such that one network is created for defaulted loans only and one for nondefaulted loans only. The idea is that a highly centralized loan in a network of defaulted loans is likely to be easily identified as defaulted. On the other hand, due to unobserved factors, loans on the periphery (i.e., less connected via observed attributes) might be impossible to identify as defaults. The same applies for a network of nondefaulted loans. After a new loan is introduced to both networks, we estimate the extent to which the loan belongs to the defaulted or nondefaulted network (see Figure 1, right panel). The given variable might be based on centralization measures and might also be optimized via k-fold cross- validation.
- In the creation of a network, it is unclear which and how many variables to use to calculate similarity distances between loans. Interestingly, this step has been left unexplored in the literature. Motivated by the success of bagging in machine learning, we would like to explore several of the previously described ideas within the following framework of multiple networks. Within this framework, we will i) randomly select m variables to create a given network; ii) find measures of interest (clusters, loan centralities for new loans, etc.); iii) repeat the steps i) and ii) n times; and iv) aggregate measures of interest across all networks. In this way, we will account for the variable choice uncertainty and inherent noisiness of the data typical of P2P lending datasets. Alternatively, we might follow a bootstrap aggregation technique:
- randomly reshuffle the training dataset;
- select predefined variables to create a given network;
- find measures of interest
- repeat steps 1 to 3 n times;
- aggregate measures of interest across all networks.
In this way, we will account for the uncertainty of the training dataset. Both approaches can be combined as well. We expect that accounting for various sources of uncertainty through aggregation will help us develop more robust network-based features, but we might also be able to understand which variables drive credit risk and what values (thresholds) of various network measures (i.e., vertex centralities) are relevant. Although these ideas represent the backbone of this research project, over the course of the three years, other new ideas are likely to emerge.
XAI methods for finance
In addition to the work on credit scoring models, we will also aim to contribute to the literature on XAI methods applied to financial problem sets. As stated previously, most of the papers available in the literature communicate the results of implementing individual post hoc XAI methods identifying the contribution of individual features to the predicted outcome. Feature importance methods provide explanations by taking a model ƒ and a point of interest x and returning a score reflecting the importance of the attributes for that specific point x. In finance, internal credit risk models are subjected to various audits (risk and legal) and have to “work” within the practical constraints under which banks operate (various unlinked database management systems, inability to transfer original client data to cloud services, etc.). Hence, for successful adoption of AI in internal risk modeling, the following three questions become crucial:
- How applicable are existing XAI methods in view of the practical constraints under which financial institutions operate? Typical loan performance datasets contain hundreds of features, and in the case of SHAP, an exact calculation of the values is computationally expensive because there are 2𝑘 possible coalitions of the feature values (where k is the number of features). In the context of this research, we will test the applicability of the different XAI methods and outline the technical specifications for a solution that can be used to directly inform end users and bring them model transparency.
- Do the explanations provided by existing techniques satisfy the intuition of risk experts concerning feature importance? In the context of our research, we will compare and interpret the explanations provided by the various XAI methods and attempt to establish a link between the individual XAI methods and the explainability needs of various financial stakeholders. For this purpose, we aim to contribute to the literature beyond the papers by Arya et al. (2019), Bhatt et al. (2020) and Berg et al. (2020). For example, in Berg et al. (2020), the authors identify the explainability needs of various stakeholders in the financial value chain but do not provide any insight into which is the best method to present such explanations.
- Are the explanations provided by the XAI methods stable and robust? We would expect loan contracts that have similar features to also have similar explanations regarding the most important features and their impact on the outcome. In this context, we can still rely on concepts from network theory to estimate a distance matrix between the loan contracts and then evaluate the robustness of the XAI methods by investigating whether loan contracts that have similar properties also have similar explanations under the various XAI methods
Contribution
The main objective of the research project is to advance our understanding of credit risk modeling in P2P lending markets by designing and empirically verifying new network-based credit risk models. Our task is to design methods suited to P2P lending market data, which are typically correlated and noisy.
The research project will lead to the following contribution:
- Methodological - With respect to the existing research (Ahelegbey et al., 2019a,b; Giudici et al., 2019; 2020), we will contribute in several aspects. First, previous methods have ignored loan status, leading to unsupervised network-based learning. However, supervised learning algorithms generally outperform unsupervised learning algorithms (Liu et al., 2020). Hence, our approach to creating the networks will utilize class information, thus leading to supervised networks. Second, in contrast to previous studies, our work acknowledges that network creation and feature extraction depend on a set of hyperparameters; their existence in turn depends on the specific way that networks and features are created. Thus, we will apply cross-validation to tune the network’s hyperparameters and resulting features. Third, previous studies have created only one network. We will also design methods to create multiple networks that will differ in two aspects:
- They will utilize different (random) sets of variables, and
- They will rely on bootstrap aggregation (bagging). We will therefore directly address data noisiness, which is ignored in the existing literature.
- Empirical – Almost all studies have used fewer than two P2P market datasets, with three datasets used only occasionally (Ha et al., 2019; Niu et al., 2020). The fourth contribution is to enrich the empirical literature, as we will be able to observe credit drivers and the usefulness of methods across different market platforms. We will use not only benchmark datasets (Lending Club and Prosper) but also new datasets from European (Zopa, Mintos, Bondora) and world (Mintos, Home Credit, Kiva) P2P markets. With this, we will be able to validate models across very different datasets capturing the unique properties of different P2P markets around the world.
- Practical – Except for a few studies (Bussmann et al. 2019, Srinivasan et al. 2019, Ariza-Garzon et al., 2020, Hadji Misheva et al. 2021 Moscato et al., 2021), the applicability and robustness of the explanations provided by existing XAI methods for credit risk models has rarely been studied. However, the future trend put forward by policymakers and regulators (through existing and planned legislation) concerning automatized solutions and P2P lending markets emphasizes the necessity of interpretable credit risk models. Thus, the fifth contribution of the proposed research project is an investigation into the applicability of existing XAI methods to credit scoring models, which will ultimately enable the development of interpretable credit risk models that can estimate not only the expected effect of each variable on the outcome but also the expected effect of each variable for a specific individual loan
References
- Ahmad, A., & Dey, L. (2007). A k-mean clustering algorithm for mixed numeric and categorical data. Data & Knowledge Engineering, 63(2), 503-527.
- Ahelegbey, D. F., & Giudici, P. (2019). Latent factor models for credit scoring in P2P systems. Physica A: Statistical Mechanics and its Applications, 522, 112-121.
- Arya, A., & Giudici, G. (2019). Network based scoring models to improve credit risk management in peer to peer lending platforms. Frontiers in Artificial Intelligence, 2, 3.
- Billio, M., Getmansky, M., Lo, A. W., & Pelizzon, L. (2012). Econometric measures of connectedness and systemic risk in the finance and insurance sectors. Journal of financial economics, 104(3), 535-559.
- Berg, J. E., Easton, P. D., Hill, M. D., & Pyzoha, S. J. (2020). XAI in the Financial Sector. A Conceptual Framework for Explainable AI.
- Blondel, V. D., Guillaume, J. L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of statistical mechanics: theory and experiment, 2008(10), P10008.
- Bhatt, P., Garg, A., & Mehta, N. (2020). Credit risk evaluation model with textual features from loan descriptions for P2P lending. Electronic Commerce Research and Applications, 42, 100989.
- Deev, O., & Lyócsa, Š. (2020). Connectedness of financial institutions in Europe: A network approach across quantiles. Physica A: Statistical Mechanics and its Applications, 550, 124035.
- Emekter, R., Tu, Y., Jirasakuldech, B., & Lu, M. (2015). Evaluating credit risk and loan performance in online Peer-to-Peer (P2P) lending. Applied Economics, 47(1), 54-70.
- Gao, X., Lu, L., & Chen, Z. (2021). Determinants of defaults on P2P lending platforms in China. International Review of Economics & Finance, 72, 334-348.
- Giudici, G., Wang, Y., & Huang, H. (2019). Network based credit risk models. Quality Engineering, 32(2), 199-211.
- He, Y., & Li, X. (2021). The failure of Chinese peer-to-peer lending platforms: Finance and politics. Journal of Corporate Finance, 66, 101852.
- Jin, Y., & Zhu, Y. (2015, April). A data-driven approach to predict default risk of loan for online peer-to-peer (P2P) lending. In 2015 Fifth International Conference on Communication Systems and Network Technologies (pp. 609-613). IEEE.
- Niu, Q., Xia, H., Li, J., & Cui, Z. (2020). Resampling ensemble model based on data distribution for imbalanced credit risk evaluation in P2P lending. Information Sciences, 536, 120-134.
- Onnela, J. P., Kaski, K., & Kertész, J. (2004). Clustering and information in correlation based financial networks. The European Physical Journal B, 38(2), 353-362.
- Robins, G., Pattison, P., Kalish, Y., & Lusher, D. (2007). An introduction to exponential random graph (p*) models for social networks. Social networks, 29(2), 173-191.
- Thakor, A. V. (2020). Fintech and banking: What do we know? Journal of Financial Intermediation, 41, 100833.
- Výrost, T., Lyócsa, Š., & Baumöhl, E. (2019). Network-based asset allocation strategies. The North American Journal of Economics and Finance, 47, 516-536.
- Wilson, D. L., & Martinez, T. R. (1997). Improved heterogeneous distance functions. Journal of artificial intelligence research, 6, 1-34.
- Xia, H., Li, J., & Niu, Q. (2017). Cost-sensitive boosted tree for loan evaluation in peer-to-peer lending. Electronic Commerce Research and Applications, 24, 30-49.